cosmuse laboratory

cosmuse laboratory

COSMUSE | cosmuse_lab | 目次 | ０ | １ | ２ | ３ | ４ | 5 | 6 | 7 | 8 | 9 |

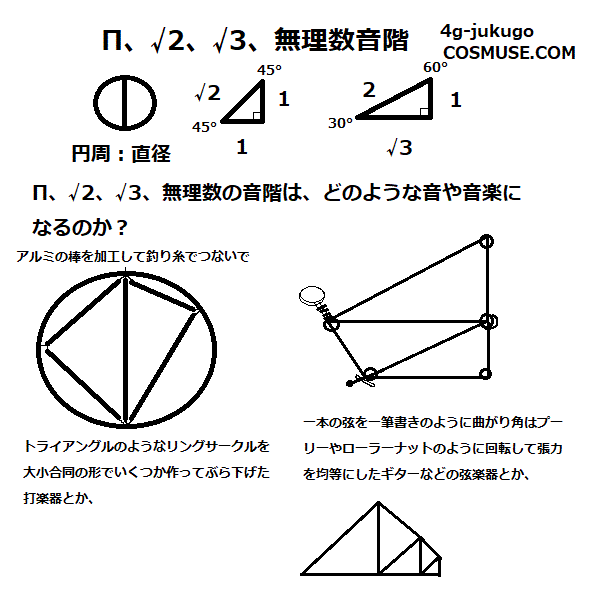
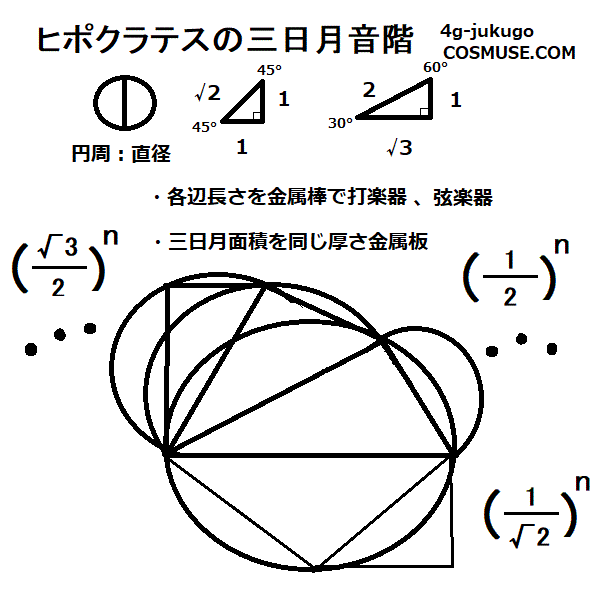
６．音階を考えてみる（自然対数の底e音階、円周率π音階、振動数周波数音階）

簡単な整数比やオクターブ、平均律12音階クロマティックスケール2^^(n/12)にこだわらず、
振動数周波数でみた場合、振動数周波数音階と考えることができるはず。
素粒子音階や周期律元素音階や電子配置や宇宙音階も
振動数周波数音階で考えれば宇宙の音楽として聞くことができるかもしれない。
（※人間の可聴周波数にピタゴラス音階(3/2)^ⁿのようにオクターブの中に
置き換える周波数変換（ダウンコンバート？）の必要があるかもしれないが…。）
（※ピタゴラス音階(3/2)^ⁿを平均律12音階クロマティックスケール2^^(n/12)に
オクターブ内にもどすために1/2、1/4、1/8、1/16、1/32、1/64…など2のn乗の逆数2^^(-n)をかけた。
または2のn乗2^ⁿで割った。
1+1/2+1/4+1/8+1/16+1/32+1/64+…の無限級数は、2に限りなく近づく。オクターブの１：２はこのためか？
これはこれで音階にできそうだ。）
だんだん、なんでもありになってきたので、
x^^(n/m)や(m/x)^ⁿなどの音階も無数に考えることができる。

６－１．自然対数の底e音階

無理数は音階にできるのか？（それとも途中で切り捨てか！？）
小数点以下が無限小数、同じ繰り返しが無いランダム。ランダムか？
自然対数の底eの音階を考えてみる。

6－1－1．自然対数の底eになるまでを音階にする

自然対数の底eなので、まず、自然対数の底eになるまでを音階にすることを考えてみる。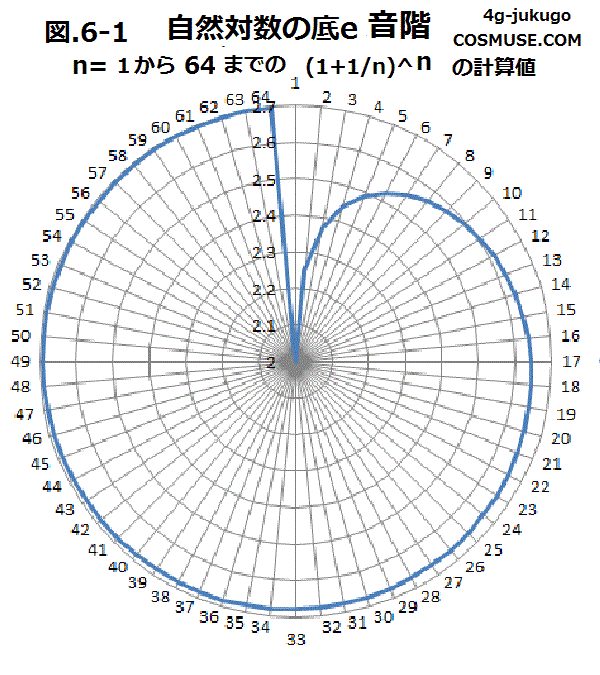
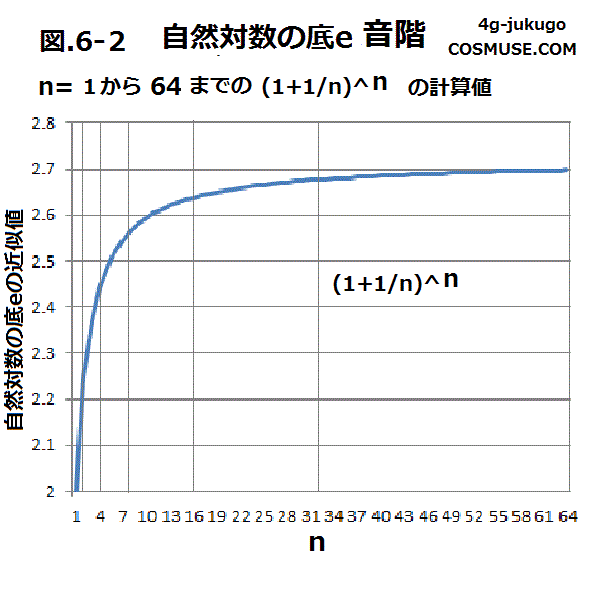
（１）自然対数の底eになるまでを音階にする１
(1+1/n)^nのｎを極大したときの値が自然対数の底e
n=1のとき(2)^1、n=2のとき(1+1/2)^2=(3/2)^2、n=3のとき(1+1/3)^3=(4/3)^3、…n=とても大きな値のときe=2.7182818…
n=1から64までグラフにしてみる。

音階がたくさん存在することになる。

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64
e	2	2.25	2.3703	2.4414	2.4883	2.5216	2.5464	2.5657	2.5811	2.5937	2.6041	2.6130	2.6206	2.6271	2.6328	2.6379	2.6424	2.6464	2.6500	2.6532	2.6562	2.6589	2.6614	2.6637	2.6658	2.6677	2.6695	2.6712	2.6728	2.6743	2.6756	2.6769	2.6782	2.6793	2.6804	2.6814	2.6824	2.6833	2.6842	2.6850	2.6858	2.6866	2.6873	2.6880	2.6886	2.6893	2.6899	2.6904	2.6910	2.6915	2.6921	2.6925	2.6930	2.6935	2.6939	2.6944	2.6948	2.6952	2.6955	2.6959	2.6963	2.6966	2.6970	2.6973

これに基準となるf₀の周波数を掛け算した周波数音階を考えることができる。
なかなかe=2.7182818…に近づかないが。
（２）自然対数の底eになるまでを音階にする２
無限級数展開して自然対数の底eになるまでを音階を考えてみる。

e^^xのx=1にした無限級数展開の式は、
e=1+1/1!+1/2!+1/3!+1/4!+1/5!+…+1/n!+…
累積していく段階は、

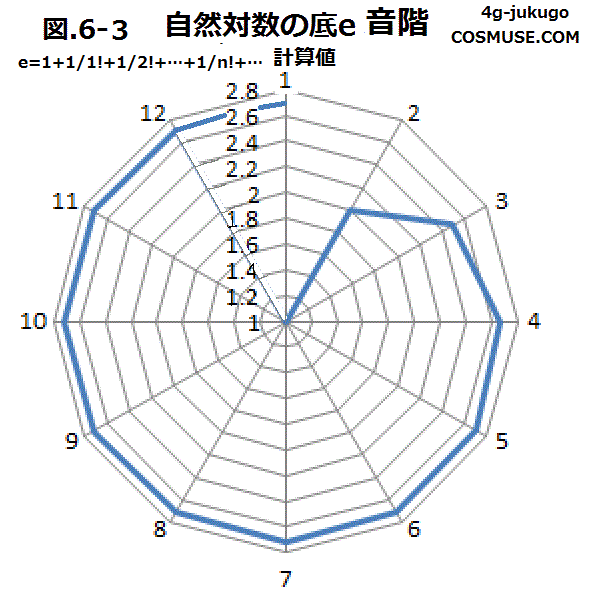
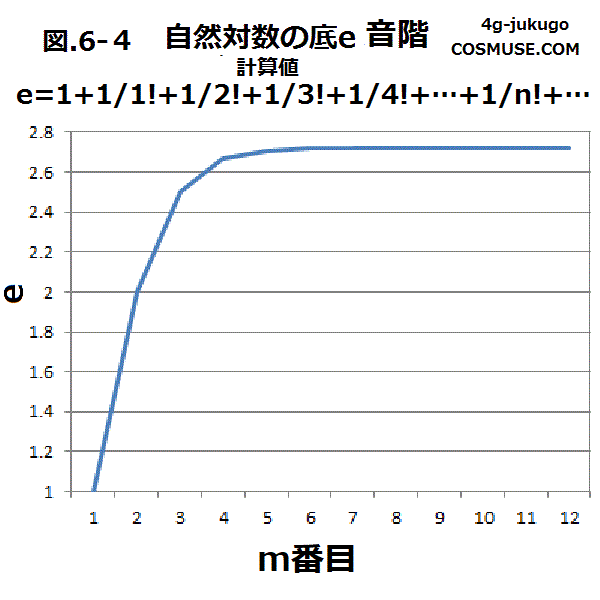
m	1	2	3	4	5	6	7	8	9	10	11	12
e	1	2	2.5	2.6666	2.7083	2.7166	2.7180	2.718253968	2.71827877	2.718281526	2.718281801	2.718281826
f₀	130.813	261.626	327.0325	348.8346667	354.2852083	355.3753167	355.5570014	355.5829563	355.5862007	355.5865612	355.5865973	355.5866005Hz

これは6番目か７番目までまたは１２音階にできるかもしれない。

6－1－2．自然対数の底eの指数関数音階

12音階クロマティックスケールは2^^(n/12)で、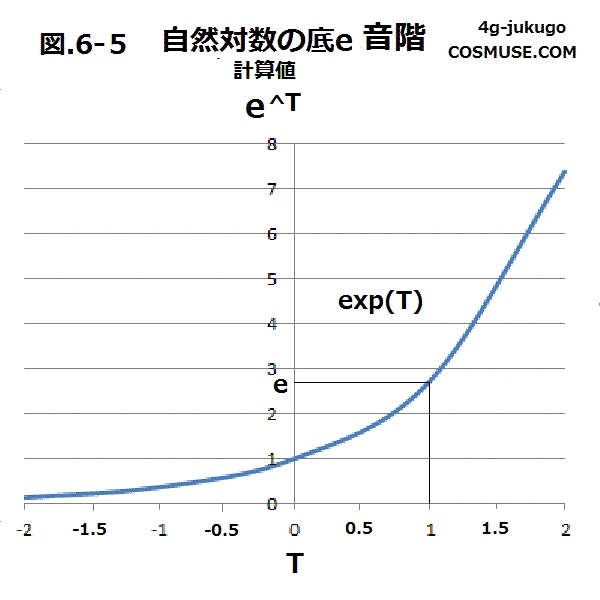
ピタゴラス音階は(3/2)^ⁿなど指数関数になっている。
自然対数の底eもそのまま指数関数で考えてみる。
e^^x
このxのところになにを置き換えるのか。
（１）πiを入れてみると、
e^^πi= -1
これはこのままでは難しそうだ…。
虚数、i^²=-1、i=√-1
電子などの対生成・対消滅や反粒子や反物質や超対称性粒子やダークマターやダークエネルギーなどを連想してしまう。
（２）PV=nRTをPV/nR=Tとして入れてみると、
e^^PV/nR=e^^T
となる。
T=0のときe^⁰=1となり、
T<0のときe^^-T=1/e^^Tという逆数になる。
excelで計算、e=2.71828182845904で計算。
（※絶対温度T(K)=273+t(℃)とか標準状態の圧力P=1.013x10^⁵[N/m^²] 、
温度T=273K　（0℃）、モル数n=質量m/分子量u、ガス定数R=0.0821[latm/molK]=8.31[J/molK]、
1molの物質中の分子数のモル分子数（アボガドロ数）6.02x10＾²³個、
0℃1気圧標準状態の理想気体1モル体積22.4リットルなどとか
熱力学の第一法則及び第二法則はおいといて…。）

T	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2
exp	0.135335283	0.22313016	0.367879441	0.60653066	1	1.648721271	2.718281828	4.48168907	7.389056099
f₀	35.40722881	58.37665128	96.24682668	158.6841904	261.626	431.3483512	711.1732017	1172.526385	1933.169191Hz

（つづく）

COSMUSE | TOP | お問い合せ