cosmuse laboratory

cosmuse laboratory

COSMUSE | cosmuse_lab | 目次 | ０ | １ | ２ | ３ | ４ | 5 | 6 | 7 | 8 | 9 |

５．自然倍音

0と1の狭間で

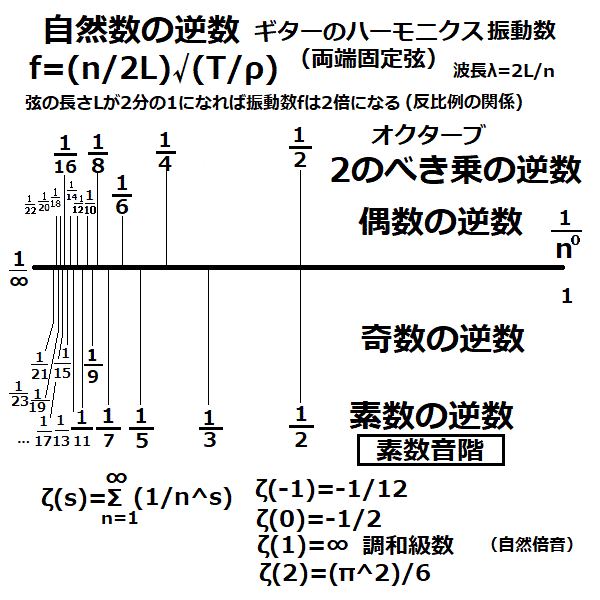
弦（両端固定）の節(node)を軽く押さえて腹(peak)をはじく、ギターハモニックスの振動は、高次の波の強さは小さく速く減衰し1/fゆらぎのもとになるのか。弦を伝わる横波の速度 v=√（T/ρ）
T：弦の張力(N)
ρ：線密度(kg/m)
自然数（正の整数）、素数、フィボナッチ数、最小公倍数、最大公約数、素因数、2や3の倍音や5度4度3度などの音でドレミファソラシドができているのか。

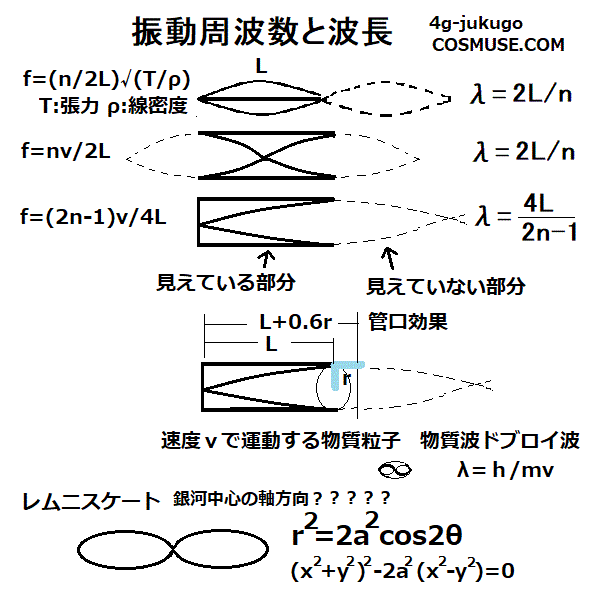
・音波の速度
圧力をPとし、密度をρとし、比熱比をｒとすると音波の速度ｖは、
ｖ＝√（ｒP/ρ）
空気中ではt℃のときの音速ｖは、
ｖ＝331.5＋0.6ｔ（m/s）
・電磁波の速度
誘電率ε(F/m)、透磁率μ(H/m)、電磁波の伝わる速度v(m/s)は
ｖ＝1／√（εμ）
振動周波数や波長は、その系のエネルギー状態、速度や質量によっても異なる。
周期律表から元素の音楽を導き出そうとすると不確定性原理やパウリの排他律や同位体などから
振動周波数のばらつきについても思慮が必要かもしれない。

両端が接続されている大小のリングは、どのような音や音階や音楽になるのか。

素数音階とフィボナッチ音階を考えるために、平均律12音階クロマチックスケールとは何か確認して、
ピタゴラス音階と自然倍音と平均律12音階クロマチックスケールを比較しているが、
そもそも自然倍音には割り切れない数がたくさん含まれている。世の中、割り切れないのか？
自然倍音には割り切れない数がたくさん含まれているが自然の音を聞いてあまり不快に思われない。
むしろ人工的な工事の音や騒音などが不快に思われることがある。（先入観、思い込み、習慣、なれなどが主観に影響するかもしれないが、）
自然倍音は周波数だけでなく
エネルギースペクトルの違いなのではないだろうか？(E=hν=hc/λ)
自然倍音に含まれる割り切れない数は抑制されている！？（E=mgh+(1/2)mv^2+(1/2)Iω^2）
聴衆者の方も不快な音が同時に入ってきても聴覚器官や意識無意識で
選別（フィルタリング）しているのかもしれないが。

５－１．自然倍音は、波や風や雨や川の流れの音や鳥や虫の音色など自然の音として聞いている。
自然倍音は１、２、３、４、５、…と整数倍の音階で直線的。ｆ(n)＝ｆ₀*ｎ
ここでは、C3を基準周波数f₀を130.813Hzとしてn=1から64まで周波数f(n)=f₀*nの計算値をグラフにすると
計算値はexcelで計算。

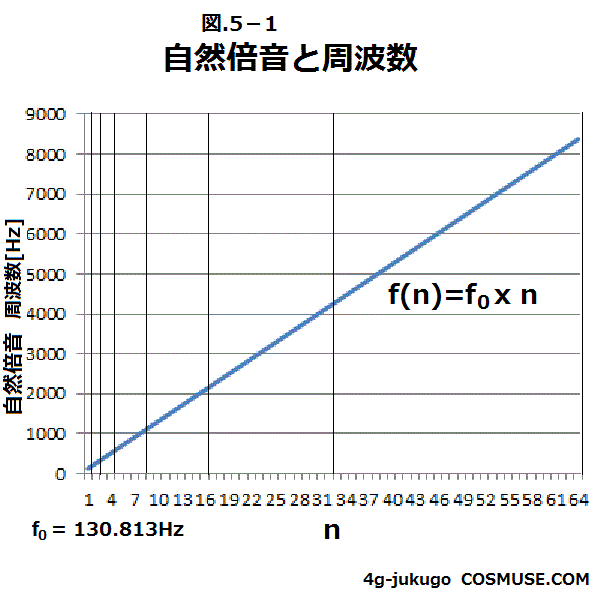
縦の線はx軸の整数nの倍（オクターブを示す線）。
n=16から32までの間には16個の音階、
n=32から64までには32個の音階が存在することになる。
表5-1.自然倍音周波数f₁

表5-1．基準周波数f₀を130.813Hzとした自然倍音の周波数f(n)と整数n=1から64まで
n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64
f₁Hz	130.813	261.626	392.439	523.252	654.065	784.878	915.691	1046.504	1177.317	1308.13	1438.943	1569.756	1700.569	1831.382	1962.195	2093.008	2223.821	2354.634	2485.447	2616.26	2747.073	2877.886	3008.699	3139.512	3270.325	3401.138	3531.951	3662.764	3793.577	3924.39	4055.203	4186.016	4316.829	4447.642	4578.455	4709.268	4840.081	4970.894	5101.707	5232.52	5363.333	5494.146	5624.959	5755.772	5886.585	6017.398	6148.211	6279.024	6409.837	6540.65	6671.463	6802.276	6933.089	7063.902	7194.715	7325.528	7456.341	7587.154	7717.967	7848.78	7979.593	8110.406	8241.219	8372.032Hz

５－２．これに対して平均律12音階クロマチックスケールは、２の指数関数的。ｆ(n)＝ｆ₀ｘ２＾^（n/12）
ここでは、C3をf₀を130.813Hzとしてn=0から64まで周波数f(n)=ｆ₀ｘ２＾^（n/12）の計算値をグラフにすると

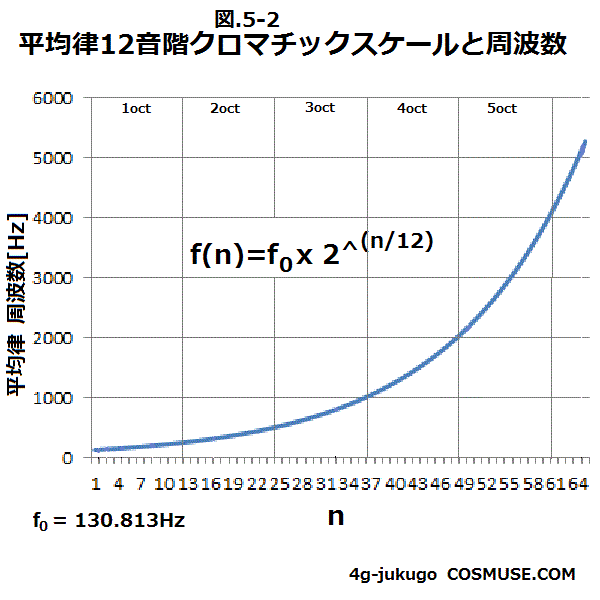
12目盛ごとの縦線はオクターブを示す。周波数は2の指数関数的に高くなる。
表5－2．平均律12音階クロマティックスケール周波数f₂

表5-2．基準周波数f0を130.813Hzとした平均律12音階クロマティックスケールの周波数f(n)と整数n=1から64まで
n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64
f₂Hz	130.813	138.5915458	146.8326279	155.5637503	164.8140523	174.6144058	184.9975187	195.9980436	207.6526938	220.0003655	233.082268	246.9420609	261.626	277.1830915	293.6652559	311.1275007	329.6281046	349.2288117	369.9950375	391.9960873	415.3053876	440.0007311	466.1645361	493.8841219	523.252	554.366183	587.3305117	622.2550013	659.2562092	698.4576234	739.9900749	783.9921746	830.6107752	880.0014621	932.3290721	987.7682437	1046.504	1108.732366	1174.661023	1244.510003	1318.512418	1396.915247	1479.98015	1567.984349	1661.22155	1760.002924	1864.658144	1975.536487	2093.008	2217.464732	2349.322047	2489.020005	2637.024837	2793.830493	2959.9603	3135.968698	3322.443101	3520.005849	3729.316289	3951.072975	4186.016	4434.929464	4698.644094	4978.040011	5274.049674Hz

５－３．自然倍音と平均律12音階クロマチックスケールをn=128番目までの計算値を比較してみる。

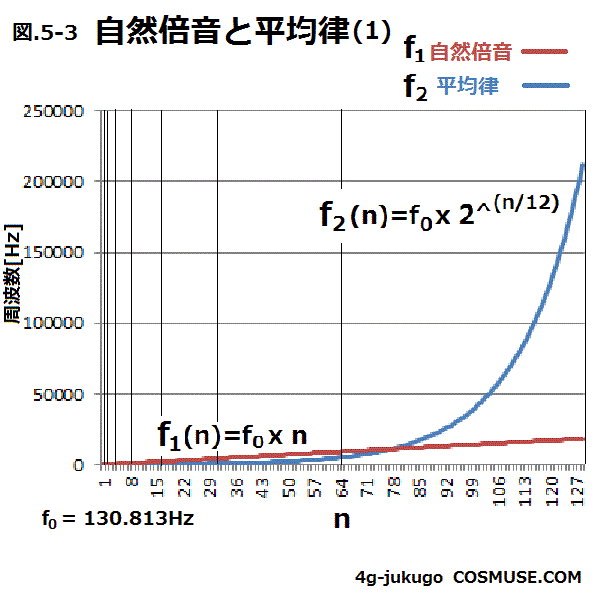
（※表は計算値データの数が多いので省く。）
同じ整数nの値での計算値の比較では整数nが低いうちは自然倍音の周波数の方がすこし高く
平均律の方が周波数低いが77番目ぐらいから平均律の方が周波数が２の指数関数的に高くなり
自然倍音の方が低くなる。
５－４．次に、
自然倍音の周波数f1に最も近い平均律12音階クロマチックスケールの周波数f₂ダッシュをn=64番目までの計算値を比較してみる。

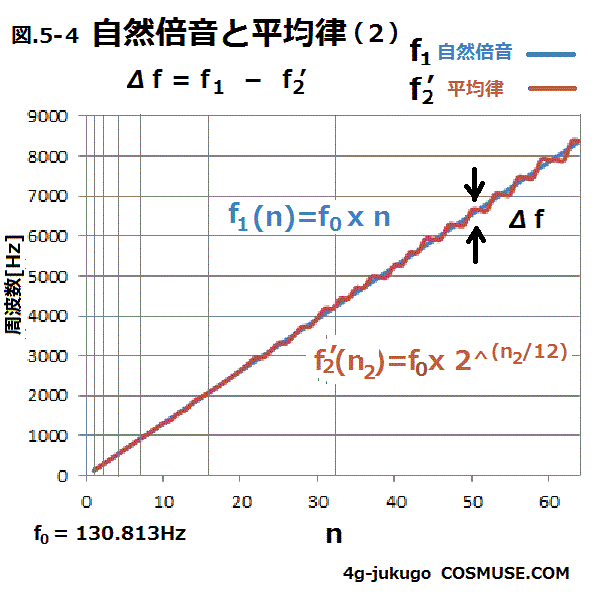
整数ｎの数が大きくなるにしたがって平均律との差が大きくなっている。
５－５．また、周波数の相関をグラフで比較してみる。

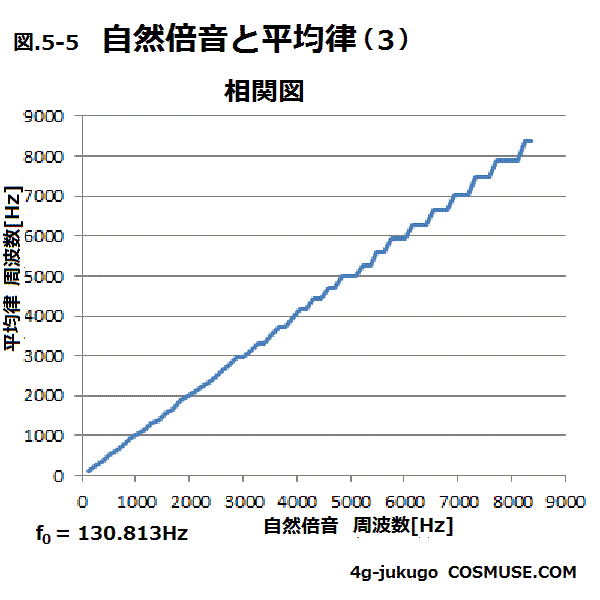
自然倍音に近い平均律周波数との偏差Δfも周波数が高くなるにしたがって大きくなる。
５－６．自然倍音に近い平均律周波数との偏差Δfをn=64番目までの計算値を比較してみる。

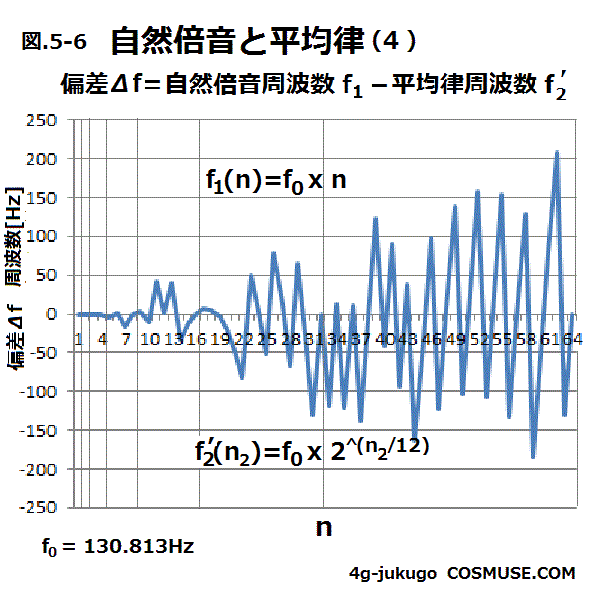
表5-6．自然倍音周波数f₁と最も近い平均律周波数f’₂の偏差Δfを整数n=1から64まで表にすると

表5-6．基準周波数f0を130.813Hzとした自然倍音の周波数f(n)と最も近い平均律12音階クロマティックスケール周波数f’₂の偏差Δfを整数n=1から64まで表示
n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64
f₁Hz	130.813	261.626	392.439	523.252	654.065	784.878	915.691	1046.504	1177.317	1308.13	1438.943	1569.756	1700.569	1831.382	1962.195	2093.008	2223.821	2354.634	2485.447	2616.26	2747.073	2877.886	3008.699	3139.512	3270.325	3401.138	3531.951	3662.764	3793.577	3924.39	4055.203	4186.016	4316.829	4447.642	4578.455	4709.268	4840.081	4970.894	5101.707	5232.52	5363.333	5494.146	5624.959	5755.772	5886.585	6017.398	6148.211	6279.024	6409.837	6540.65	6671.463	6802.276	6933.089	7063.902	7194.715	7325.528	7456.341	7587.154	7717.967	7848.78	7979.593	8110.406	8241.219	8372.032Hz
f’₂	130.813	261.626	392.439	523.252	659.2562092	783.9921746	932.3290721	1046.504	1174.661023	1318.512418	1396.915247	1567.984349	1661.22155	1864.658144	1975.536487	2093.008	2217.464732	2349.322047	2489.020005	2637.024837	2793.830493	2959.9603	2959.9603	3135.968698	3322.443101	3322.443101	3520.005849	3729.316289	3729.316289	3951.072975	4186.016	4186.016	4434.929464	4434.929464	4698.644094	4698.644094	4978.040011	4978.040011	4978.040011	5274.049674	5274.049674	5587.660987	5587.660987	5919.9206	5919.9206	5919.9206	6271.937397	6271.937397	6271.937397	6644.886202	6644.886202	6644.886202	7040.011697	7040.011697	7040.011697	7458.632577	7458.632577	7458.632577	7902.14595	7902.14595	7902.14595	7902.14595	8372.032	8372.032Hz
ΔfHz	0	0	0	0	-5.1912092	0.88582541	-16.63807213	0	2.655976596	-10.3824184	42.02775325	1.77165082	39.34744951	-33.27614426	-13.34148744	0	6.356267801	5.311953192	-3.573005358	-20.7648368	-46.7574935	-82.07429976	48.73870024	3.54330164	-52.11810098	78.69489902	11.94515141	-66.55228851	64.26071149	-26.68297487	-130.813	0	-118.1004644	12.7125356	-120.1890936	10.62390638	-137.9590107	-7.146010715	123.6669893	-41.5296736	89.2833264	-93.51498699	37.29801301	-164.1485995	-33.33559951	97.47740049	-123.7263967	7.086603281	137.8996033	-104.236202	26.57679804	157.389798	-106.9226972	23.89030281	154.7033028	-133.104577	-2.29157703	128.521423	-184.1789497	-53.36594975	77.44705025	208.2600503	-130.813	0Hz

５－７．自然倍音に近い平均律周波数との偏差をn=16番目までの計算値を比較してみる。

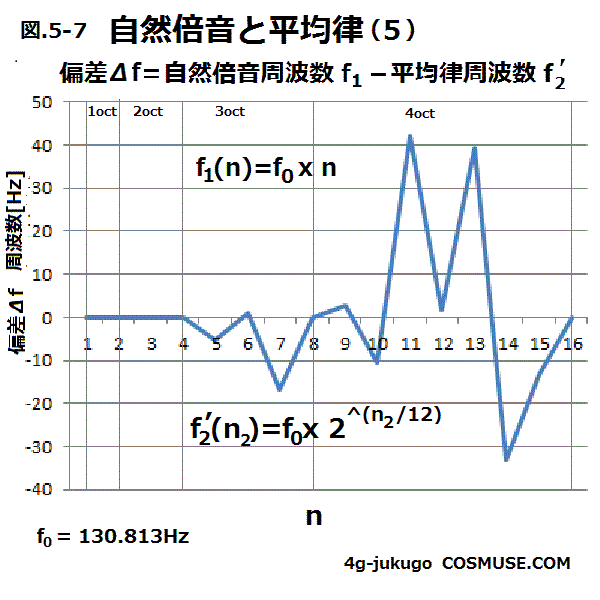
表5-7．自然倍音周波数f₁と最も近い平均律周波数f’₂との偏差Δf（Hz）。

表5-7．基準周波数f₀を130.813Hzとした自然倍音の周波数f(n)と最も近い平均律12音階クロマティックスケール周波数f’₂の偏差Δfを整数n=1から16まで表示
n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
f₁	130.813	261.626	392.439	523.252	654.065	784.878	915.691	1046.504	1177.317	1308.13	1438.943	1569.756	1700.569	1831.382	1962.195	2093.008Hz
f’₂	130.813	261.626	392.439	523.252	659.2562092	783.9921746	932.3290721	1046.504	1174.661023	1318.512418	1396.915247	1567.984349	1661.22155	1864.658144	1975.536487	2093.008Hz
ΔfHz	0	0	0	0	-5.1912092	0.88582541	-16.63807213	0	2.655976596	-10.3824184	42.02775325	1.77165082	39.34744951	-33.27614426	-13.34148744	0Hz

これらのずれの出る数やずれ方が素数やフィボナッチ数列と関係があるように見える。

５－６．ピタゴラス音階、純正律、自然倍音、平均律の音階隣接差比較

ピタゴラス音階、純正律、自然倍音、平均律の音階隣接差を比較する。
音階隣接差周波数Δf(Hz)とは隣り合う音階の周波数差で音階周波数f(n)-音階周波数f(n-1)で計算した。
ここでは、基準周波数f₀を130.813Hzとして計算した。C3

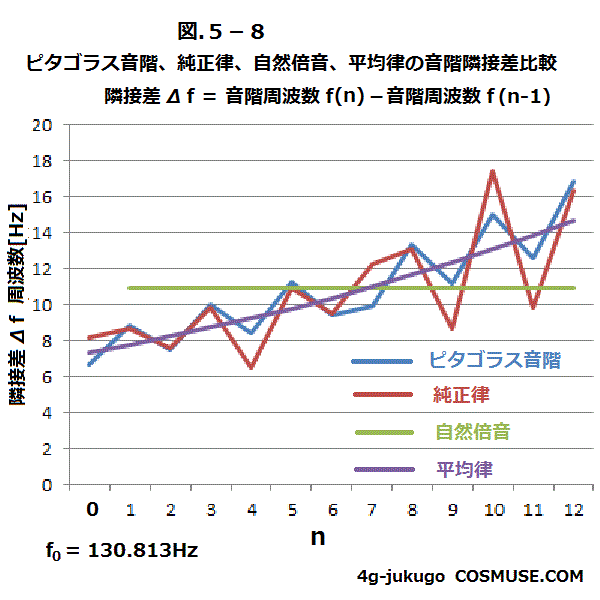
各音階の周波数の隣接差を比較すると純正律が最も隣接差も上下大きくばらつきも大きいので転調に弱いと思われるが
転調のときも演奏者は瞬時に次の調の純正律に合わせることができているのではないだろうか？
声楽やフレットレスのヴァイオリンなどには上限下限の周波数を除いては音階の制限はないと思われる。
計算上の周波数では各音階との周波数の差があるが演奏者や聴衆者は周波数で聴いているというよりも
よりよい響きで聴いているのではないだろうか？
DTMでは、もっぱら作曲ソフト頼りで…。

５－７．音楽のイメージ（万華鏡お花畑）

つまるところ、音階とはなんなのだろうか？

１：２や２：３など簡単な整数比や2つ以上の音程の響きから
長い歴史を経て転調にも様々な楽器との合奏にも対応できる
現在の平均律12音階クロマティックスケールが市民権を得たといえる。

もし、AI（人工知能）が、意思をもって音楽をつくったり聴いたりしたと仮定して
その時何が起きているのかを想像すると。

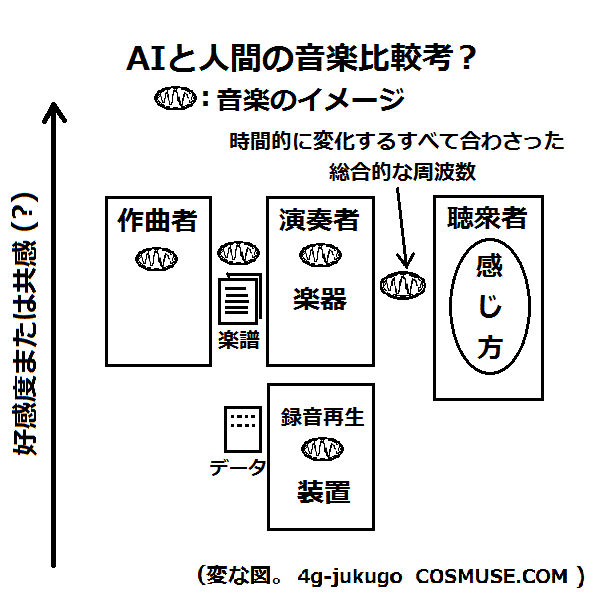
つくられた音楽が音として出ているとき、それを聴衆者が聞いているときの
時間的に変化するすべて合わさった総合的な周波数がどうなっているのだろうか？。

人間の場合は、歌（言語）やメロディーを楽器と弾いたり鼻歌を録音したり
五線紙に書いたりして作曲してそれを演奏したり歌われたりして、
さまざまな音楽に携わる人々の仕事と想いの上に
最終的に時間的に変化するすべて合わさった総合的な周波数ができあがる。

つまり、もしAIが音楽をつくるとき、いきなり時間的に変化するすべて合わさった総合的な周波数を
つくるのではないのか？という可能性を考えることができる。

つぎに、時間的に変化するすべて合わさった総合的な周波数を
意思を持ったAIがどのように聴くのか？感じるのか？解析分析するのか？
音にも出さず2進法のデジタル生データを解析分析するのだろうか？
（AI同士なら2進法の機械語デジタルデータのままでデータ入出力するのか？
量子コンピュータでは2進法デジタルではなく同時に結果が出る、同時同一労働同一対価！？
そもそもAI同士ではなくAIひとつと計算されてしまうのだろうか？）
どんな音に変化していってしまうのか？進化なのか？それを人間がどのように理解できるのか？

また、時間的に変化するすべて合わさった総合的な周波数データだけが音楽なのか？そうではないと考えているが。

そして、音楽の進化とは何か？（哲学的に悩むとなかなか先に進まない？）

さらに、音楽を聴いているときの人間なら感じ方、感情などがどのように頭の中で科学的変化が起きているのか？

逆に頭の中の科学的変化を聴衆者の頭の中で聴衆者が
思うままに理想を感じたりヴァーチャル体験できるまたは装置ができるとすると
禅やヨガや瞑想などでのように心の平和が訪れるのか？それとも理想達成感からやる気がなくなってしまうのか？

万華鏡お花畑という新しい楽譜をAI（人工知能）であればどのように音や音楽にするのだろうか？
万華鏡お花畑 cosmuse.net

５－８．弦と管の出す音

波動の公式
振動数（周波数）をｆとし、周期をTとし、波長をλとすると波の伝わる速さｖは、
ｖ＝λ/T
ｆ＝1/Tなので
ｖ＝λ/T＝λｆ
振動数（周波数）は、ある点の振動が1秒間にｆ回繰り返される場合の振動数（周波数）をｆ（Hz）。
音波の速度
圧力をPとし、密度をρとし、比熱比をｒとすると音波の速度ｖは、
ｖ＝√（ｒP/ρ）
空気中ではt℃のときの音速ｖは、
ｖ＝331.5＋0.6ｔ（m/s）
可聴音は振動数（周波数）約20Hzから16000Hzといわれている。
弦を伝わる横波の速さ
弦の張力をTとし、線密度をρとすると速さｖは、
ｖ＝√（T/ρ）
張力Tの単位は（Nニュートン）、線密度ρの単位は、弦の単位長さの質量（kg/m）。

両端がとめられた弦、または、両端が開あるいは両端が閉じている管の出す音は、
弦あるいは管の長さをLとして、定在波の波長をλとすると
λ＝２L/n
となる、
ここで、nは、腹または節の数、整数n=1、2、3、…。
両端ではなく、
一方だけが開または一方だけが閉じている管の出す音は、
λ＝４L/(2n+1)
となる、
ここで、nは、腹または節の数、整数n=1、2、3、…。
定在波の腹から腹（または節から節）までの距離は波長λ/2となる。

弦の固有振動
弦の長さをL（ｍ）とし、張力をT（N)とし、線密度をρ（kg/m）とすると固有振動数ｆ（Hz）は、
ｆ＝(n/2L)√（T/ρ）
となる。
気柱の固有振動
一方が閉じている場合、管の長さをL（ｍ）とし、音の速度をｖ（m/s）とすると固有振動数ｆ（Hz）は、
ｆ＝（2n-1）v/4L
両端が開いている場合、管の長さをL（ｍ）とし、音の速度をｖ（m/s）とすると固有振動数ｆ（Hz）は、
ｆ＝n v/2L
となる、
ここで、nは、腹または節の数、整数n=1、2、3、…。
波の重ね合わせの原理によってまさに自然倍音ができている。

自然倍音が、どんな音や音楽になるのかを何十本も弦を張って確認したかったが
長さ以外に周波数や張力や線密度を測りながら楽器にする測定器や方法を思いつかず
かわりに直径５ｍｍほどのアルミの約１ｍの円柱の棒を何本も購入し長さを何本も
自然倍音になるように整数の逆数の長さに切って釣り糸でぶら下げて途中まで制作していたが
これも3.11で途中で塩漬けになっている。
1/1、1/2、1/3、1/4、1/5、1/6、1/7、1/8、1/9、1/10、1/11、1/12、1/13、1/14、…1/63、1/64までの比。

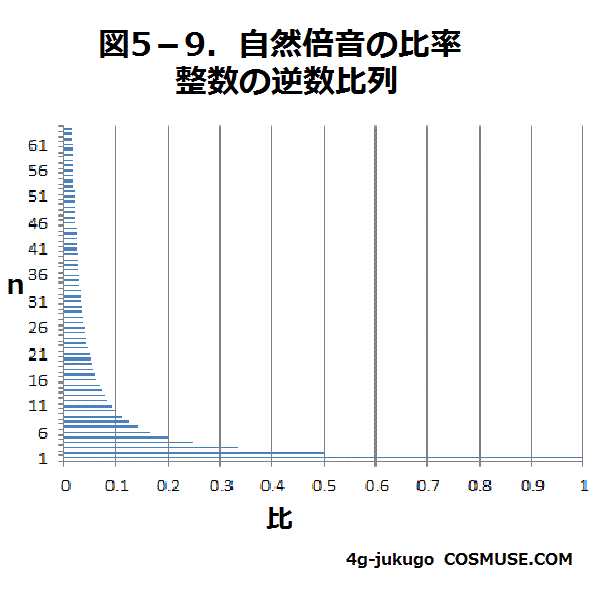
これまで、宇宙音楽として新規の楽器、新規の音楽、新しい音階を模索してきましたが、現在のドレミファソラシド、半音12音階が、物理的にも数学的にも理にかなっているので逸脱するのは難しいようです。
物理的、波の腹と節、整数倍、倍音、共振、
数学的、たとえば10進数では1桁下がれば10分の1に小さくなる。自然数が小数より大きい。最小公倍数、最大公約数、素因数。

地球上（万有引力の下）で水面に水滴が一滴落ちるとき（片側固定？）の時間的に超スローモーションは、落ちた瞬間の衝撃で最初の波紋ができ、
水滴が水中に消え、クレーターと王冠ができ２番目の波紋ができる、完全な対称にはなりにくい王冠の複数の突起状にそれぞれ小さな水滴ができ、
王冠が外側に崩れて新たな波紋ができ、中心のクレーターは水面に水平に戻るときに中心に周囲からぶつかる衝撃で中心がもりあがり
上に向かって水滴がはねる、中心部の山は水平に戻ろうとして波紋ができ、はねた水滴がまた落ちて再び波紋ができる減衰振動になり、
最初の衝撃から複数の波紋ができる。均一な同心円にはならない。
一方向からの衝撃ではなく宇宙空間でのビッグバンの場合は、時空の振動的広がりになるのか？
渦や軸ができる場合、中心震動から軸方向と直角の渦巻き方向とその間の時空の性質が異なるのだろうか？物質、反物質、暗黒物質、ダークエネルギー？
エネルギー保存則は、位置エネルギーmgh＋運動エネルギーmv^2/2＋回転運動エネルギーIω^2/2＝一定、成り立っているのだろうか？

地球の重力の及ばないところ、宇宙や非常に小さな小さな空間では、弦の両端が固定されていなくても、
または両端がつながった輪ゴムのような弦も振動しているとすれば、どのような振動だろうか？
不規則なのかばらつきがあるのか規則性があるのだろうか？
振動を可聴範囲に変換するとどのような音楽になるのだろうか？

（つづく）

COSMUSE | TOP | お問い合せ