
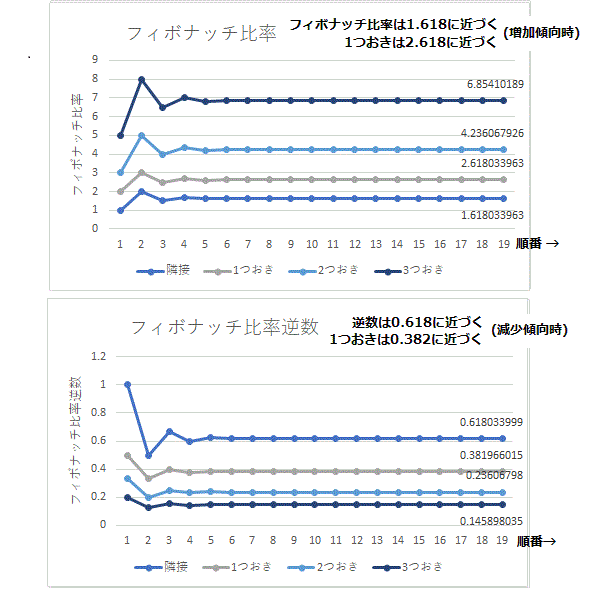
フィボナッチ漸化式 an+2=an+1+an
一般項 an=(1/√5)[((1+√5)/2)n-((1-√5)/2)n]
素数音階とフィボナッチ音階を考えてみます。どのような音や音楽になるのか。
ここまで画数音階、ひらがな音階、植木算音階などを平均律12音階クロマチックスケールにあてはめてきましたが
素数音階とフィボナッチ音階を考えるために、平均律12音階クロマチックスケールとは何か確認して、 ピタゴラス音階と自然倍音と平均律12音階クロマチックスケールを比較してみます。
4.音階を考えてみる4(素数音階、フィボナッチ音階)


フィボナッチ漸化式 an+2=an+1+an
一般項 an=(1/√5)[((1+√5)/2)n-((1-√5)/2)n]
素数音階とフィボナッチ音階を考えてみます。どのような音や音楽になるのか。
ここまで画数音階、ひらがな音階、植木算音階などを平均律12音階クロマチックスケールにあてはめてきましたが
素数音階とフィボナッチ音階を考えるために、平均律12音階クロマチックスケールとは何か確認して、
ピタゴラス音階と自然倍音と平均律12音階クロマチックスケールを比較してみます。
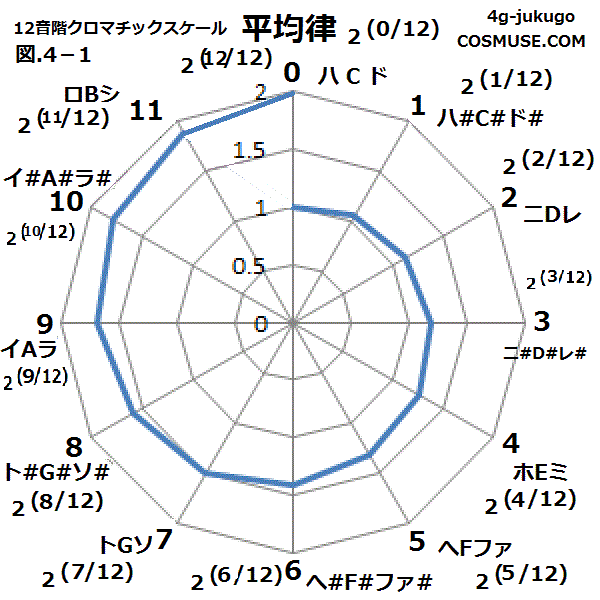
4−1.12音階クロマチックスケール(平均律)
オクターブを2(0/12)=1、2(1/12)、2(2/12)、2(3/12)、2(4/12)、2(5/12)、2(6/12)、2(7/12)、2(8/12)、2(9/12)、2(10/12)、2(11/12)、2(12/12)=2と12等分し、
これに基準の周波数に掛けたり弦の長さを割ったりしてそれぞれの音階の周波数や弦の長さがきまる。
半音の幅が等しく隣同士の誤差も最小なので転調に強いがドミソなどの和音コードの響きは純正律に劣るといわれている。
ドレミフャとabcとイロハとややこしいので表と時計回りの図にしてみる。
※正しい表記法や誤りには後でその都度修正します。長短入りました。
放射軸目盛は比率、時計回りは次数、周波数はHz、excelで計算、小数点4桁以下は切り捨て表示。
4-1-1.A(ラ)からはじまる12音階クロマチックスケール
チューニングはA(ラ)で合わせることが多い。| イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | い |
| a | a# | b | c | c# | d | d# | e | f | f# | g | g# | a’ |
| ラ | ラ# | シ | ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ら |
| 2(0/12)=1 | 2(1/12) | 2(2/12) | 2(3/12) | 2(4/12) | 2(5/12) | 2(6/12) | 2(7/12) | 2(8/12) | 2(9/12) | 2(10/12) | 2(11/12) | 2(12/12)=2 |
| 440.000 | 466.163 | 493.883 | 523.251 | 554.365 | 587.329 | 622.253 | 659.255 | 698.456 | 739.988 | 783.990 | 830.609 | 880.000Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4-1-2.C(ド)からはじまる12音階クロマチックスケール
鍵盤楽器は、c(ド)を中心にすることが多い。| ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ | は |
| c | c# | d | d# | e | f | f# | g | g# | a | a# | b | c’ |
| ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | ド |
| 2(0/12)=1 | 2(1/12) | 2(2/12) | 2(3/12) | 2(4/12) | 2(5/12) | 2(6/12) | 2(7/12) | 2(8/12) | 2(9/12) | 2(10/12) | 2(11/12) | 2(12/12)=2 |
| C3 130.813 | 138.591 | 146.832 | 155.563 | 164.814 | 174.614 | 184.997 | 195.998 | 207.652 | 220.000 | 233.082 | 246.942 | 261.626Hz |
| C4 261.626 | 277.183 | 293.665 | 311.127 | 329.628 | 349.228 | 369.995 | 391.996 | 415.305 | 440.000 | 466.164 | 493.884 | 523.252Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4-1-3. E(ミ)からはじまる12音階クロマチックスケール
ギターは、EADGBEにチューニングすることが多い。弦の長さcm| ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ほ |
| e | f | f# | g | g# | a | a# | b | c | c# | d | d# | e’ |
| ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | ド | ド# | レ | レ# | ミ |
| 2(0/12)=1 | 2(1/12) | 2(2/12) | 2(3/12) | 2(4/12) | 2(5/12) | 2(6/12) | 2(7/12) | 2(8/12) | 2(9/12) | 2(10/12) | 2(11/12) | 2(12/12)=2 |
| 1弦329.628 | 349.228 | 369.995 | 391.996 | 415.305 | 440.000 | 466.164 | 493.884 | 523.252 | 554.366 | 587.330 | 622.255 | 659.256Hz |
| 2弦246.941 | 261.625 | 277.182 | 293.664 | 311.127 | 329.627 | 349.228 | 369.994 | 391.995 | 415.304 | 440.000 | 466.163 | 493.883Hz |
| 3弦196.000 | 207.652 | 220.000 | 233.081 | 246.941 | 261.625 | 277.182 | 293.664 | 311.127 | 329.627 | 349.228 | 369.994 | 391.995Hz |
| 4弦146.837 | 155.563 | 164.813 | 174.614 | 184.997 | 195.997 | 207.652 | 220.000 | 233.081 | 246.941 | 261.625 | 277.182 | 293.664Hz |
| 5弦110.000 | 116.540 | 123.470 | 130.812 | 138.591 | 146.832 | 155.563 | 164.813 | 174.614 | 184.997 | 195.997 | 207.652 | 220.000Hz |
| 6弦 82.41 | 87.31 | 92.50 | 98.00 | 103.830 | 110.000 | 116.545 | 123.475 | 130.817 | 138.596 | 146.837 | 155.569 | 164.820Hz |
| 長さ 630.000 | 594.640 | 561.266 | 529.764 | 500.031 | 471.966 | 445.477 | 420.474 | 396.875 | 374.600 | 353.575 | 333.730 | 315.000cm |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
なぜ12なのか?
円の内接する正三角形の中に内接する円のなかに内接する正四角形の中に内接する円のなかに内接する正五角形のなかに…
を繰り返していくと正多角形が限りなく円に近付きその円の直径は最初の外円の12分の1に近似するらしい。
ピタゴラスも当然このことを知っていて現代の12音階になったのではないかとも思ってしまう。
単純に、1:2と2:3から始まった音階は、1x2x2x3=12なので12音階かもしれない。
ところが3が入っている。1/3、2/3、1/5、1/6、1/7、1/9、1/11、…など割り切れない数が入っているために
割り切れない音階になっているのかもしれない。3は、最も小さい奇数で素数。
有名なピタゴラスの定理(内角に一つの直角を含む三角形の辺の比)は、1:1:√2、1:2:√3、3:4:5、
斜辺の二乗は他の二辺の二乗の和に等しい。
r^2=y^2+x^2
原点を中心とした半径rの円の方程式でもある。
歴史的には、宇宙は138億年、地球は46億年、およそ700万年前人類発祥はアフリカといわれている。スマホもネットもテレビもラジオもない太古の昔には、夜は月と星の天体ショー、昼は太陽、雲、雨、風。
生きていくための衣食住。まず体温を保護する衣類、つぎに水、食糧、狩猟、遊牧、
農作が始まってからは定住住居を必要とされたと想像する。
古代エジプト、古代メソポタミア文明シュメール、古代インド、古代黄河、古代マヤなどの頃も、月を見て地球(の影)が丸いことを知っていたはず。
月の満ち欠けから太陰暦で12か月、1年で太陽を地球が一回りで太陽暦、から
12進法、1週間7日や60進法の時間の単位や月や地球の影が丸いことから円周360°などを使っていたはず。
日常的には10進法の方が古いといわれているが。
人類は、本能的に周期Tは、振動が1往復する時間であることも、
振動数または周波数fの逆数のことも知っていたのではないだろうか。
???
数列、無限級数、極限値、収束、発散∞、振動(規則性振動、不規則振動)、変曲点、微分、積分、テーラー展開、フーリエ級数、モンテカルロ法などについて、
ん十年前の小学校の時、先生が「1+2+3+…を無限大の総和はいくつになるか?」という問題が出て、
誰も答えられないとしばらくして「−12分の1になることを誰か説明できる人?」この12のことか?
(ゼータ関数や解析接続についてもっと勉強しなくては…)
正の整数の1に1の半分の半分の半分の…それぞれ足した無限級数和では、
1+1/2+1/4+1/8+1/16+1/32+1/64+… =2
プラスマイナス交代無限級数和では、
1-1/2+1/4-1/8+1/16-1/32+1/64-… =2/3
1に3分の1の3分の1の3分の1の…それぞれ足した無限級数和では、
1+1/3+1/9+1/27+1/81+1/243+1/729+… =3/2
プラスマイナス交代無限級数和では、
1-1/3+1/9-1/27+1/81-1/243+1/729-… =3/4
arctan 1
=1-1/3+1/5-1/7+1/9-1/11+…=π/4
ζ(2)
=1+1/2^2+1/3^2+1/4^2+1/5^2+1/6^2+1/7^2+1/8^2+1/9^2+…=π^2/6
交代調和級数
1-1/2+1/3-1/4+1/5-1/6+1/7-1/8+…=ln2
ζ(1) 調和級数
=1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+…=∞
ζ(-1)
=1+2+3+4+5+6+7+8+…=-1/12
ζ(0)=-1/2
4−2.ピタゴラス音階
ピタゴラス音階は、1:2のオクターブと2:3の5度によって、 5度を積み上げて音階がつくられ純正完全5度音階を12回積み上げると60度となる。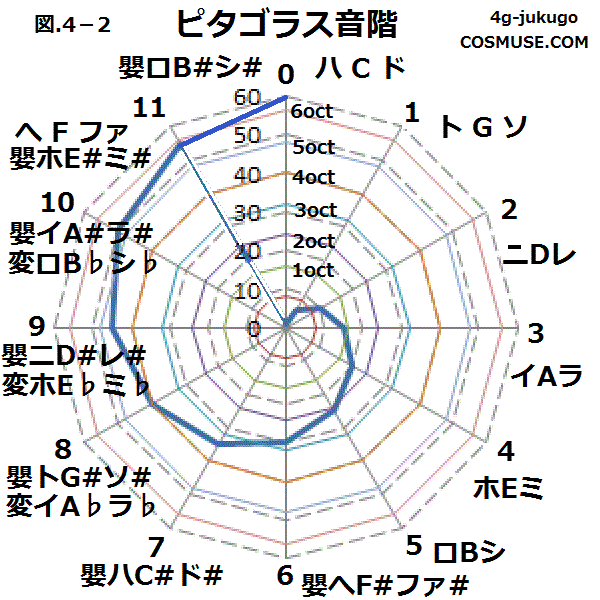
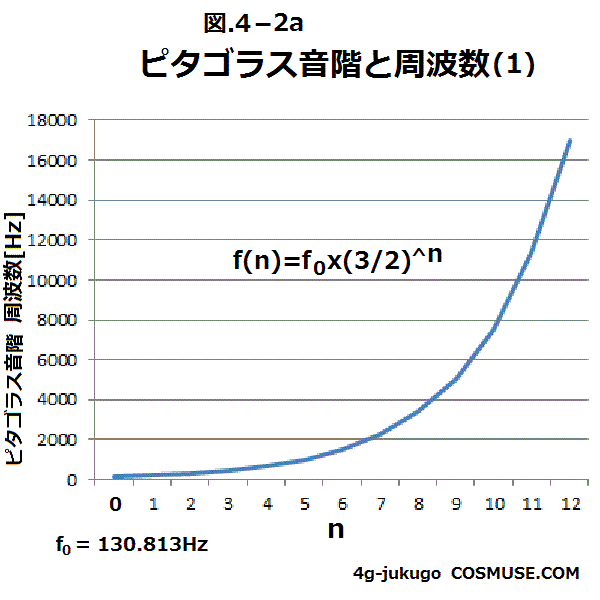
4−2−1.C(ド)からピタゴラス音階
| ハ | ト | 二 | イ | ホ | ロ |
嬰へ 変ト |
嬰ハ 変ニ |
嬰ト 変イ |
嬰二 変ホ |
嬰イ 変ロ | へ |
は 嬰ロ |
| c | g | d | a | e | b | f# | c# | g# | d# | a# | f | b# |
| ド | ソ | レ | ラ | ミ | シ | ファ# | ド# | ソ# | レ# | ラ# | ファ | シ# |
| (3/2)0=1 | (3/2)1 | (3/2)2 | (3/2)3 | (3/2)4 | (3/2)5 | (3/2)6 | (3/2)7 | (3/2)8 | (3/2)9 | (3/2)10 | (3/2)11 | (3/2)12 |
| 261.626 | 392.439 | 588.658 | 882.987 | 1324.481 | 1986.722 | 2980.083 | 4470.125 | 6705.188 | 10057.782 | 15086.673 | 22630.010 | 33945.015Hz |
| 1 | 1 | 1/2 | 1/2 | 1/4 | 1/4 | 1/8 | 1/16 | 1/16 | 1/32 | 1/32 | 1/64 | 1/64 |
| 261.626 | 392.439 | 294.329 | 441.493 | 331.120 | 496.680 | 372.510 | 279.382 | 419.074 | 314.305 | 471.458 | 353.593 | 530.390Hz |
| # | ## | ### | #### | ##### bbbbbbb | ###### bbbbbb | bbbbb ####### | bbbb | bbb | bb | b |
| ハ |
嬰ハ 変ニ | 二 |
嬰二 変ホ | ホ | へ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ |
は 嬰ロ |
| c | c# | d | d# | e | f | f# | g | g# | a | a# | b | b# |
| ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | シ# |
| 261.626 | 279.382 | 294.329 | 314.305 | 331.120 | 353.593 | 372.510 | 392.439 | 419.074 | 441.493 | 471.458 | 496.680 | 530.390Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
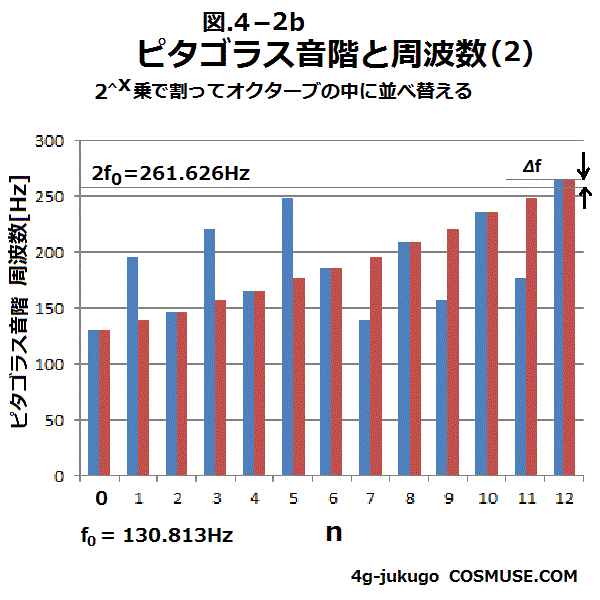
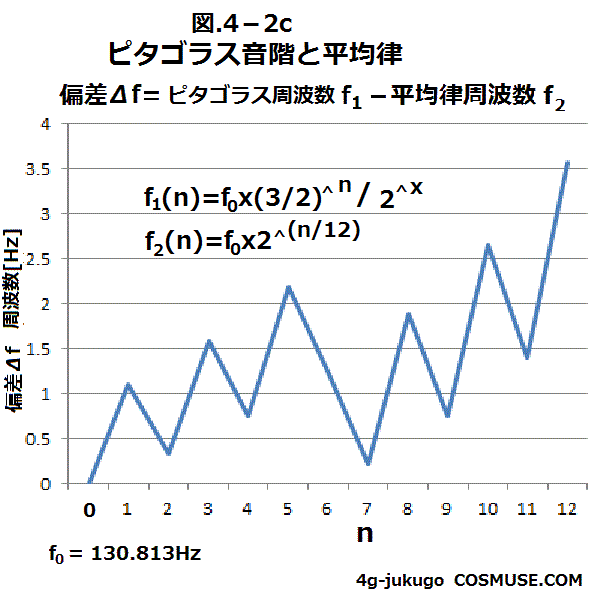
4−2−2.A(ラ)からピタゴラス音階
| イ | ホ | ロ |
嬰へ 変ト |
嬰ハ 変ニ |
嬰ト 変イ |
嬰二 変ホ |
嬰イ 変ロ | へ | ハ | ト | 二 | い |
| a | e | b | f# | c# | g# | d# | a# | f | c | g | d | a’ |
| ラ | ミ | シ | ファ# | ド# | ソ# | レ# | ラ# | ファ | ド | ソ | レ | ら |
| (3/2)0=1 | (3/2)1 | (3/2)2 | (3/2)3 | (3/2)4 | (3/2)5 | (3/2)6 | (3/2)7 | (3/2)8 | (3/2)9 | (3/2)10 | (3/2)11 | (3/2)12 |
| 440.000 | 660.000 | 990.000 | 1485.000 | 2227.500 | 3341.250 | 5011.875 | 7517.812 | 11276.718 | 16915.078 | 25372.617 | 38058.925 | 57088.388Hz |
| 1 | 1 | 1/2 | 1/2 | 1/4 | 1/4 | 1/8 | 1/16 | 1/16 | 1/32 | 1/32 | 1/64 | 1/64 |
| 440.000 | 660.000 | 495.000 | 742.500 | 556.875 | 835.312 | 626.484 | 469.863 | 704.794 | 528.596 | 792.894 | 594.670 | 892.006Hz |
| イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | 二 |
嬰二 変ホ | ホ | へ |
嬰へ 変ト | ト |
嬰ト 変イ | い |
| a | a# | b | c | c# | d | d# | e | f | f# | g | g# | a' |
| ラ | ラ# | シ | ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ら |
| 440.000 | 469.863 | 495.000 | 528.596 | 556.875 | 594.670 | 626.484 | 660.000 | 704.794 | 742.500 | 792.894 | 835.312 | 892.006Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4−2−3.E(ミ)からピタゴラス音階
| ホ | ロ |
嬰へ 変ト |
嬰ハ 変ニ |
嬰ト 変イ |
嬰二 変ホ |
嬰イ 変ロ | へ | ハ | ト | 二 | イ | ほ |
| e | b | f# | c# | g# | d# | a# | f | c | g | d | a | e’ |
| ミ | シ | ファ# | ド# | ソ# | レ# | ラ# | ファ | ド | ソ | レ | ラ | み |
| (3/2)0=1 | (3/2)1 | (3/2)2 | (3/2)3 | (3/2)4 | (3/2)5 | (3/2)6 | (3/2)7 | (3/2)8 | (3/2)9 | (3/2)10 | (3/2)11 | (3/2)12 |
| 329.628 | 494.442 | 741.663 | 1112.494 | 1668.741 | 2503.112 | 3754.668 | 5632.003 | 8448.005 | 12672.007 | 19008.011 | 28512.017 | 42768.025Hz |
| 1 | 1 | 1/2 | 1/2 | 1/4 | 1/4 | 1/8 | 1/16 | 1/16 | 1/32 | 1/32 | 1/64 | 1/64 |
| 329.628 | 494.442 | 370.831 | 556.247 | 417.185 | 625.778 | 469.333 | 352.000 | 528.000 | 396.000 | 594.000 | 445.500 | 668.250Hz |
| ホ | へ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | 二 |
嬰二 変ホ | ほ |
| e | f | f# | g | g# | a | a# | b | c | c# | d | d# | e' |
| ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | ド | ド# | レ | レ# | み |
| 329.628 | 352.000 | 370.831 | 396.000 | 417.185 | 445.500 | 469.333 | 494.442 | 528.000 | 556.247 | 594.000 | 625.778 | 668.250Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4−3.純正律
純正律は、オクターブの中のド、レ、ミ、ファ、ソ、ラ、シ、ドを簡単な整数比の1、9/8、5/4、4/3、3/2、5/3、15/8、2の整数比で構成された音階。
オクターブ1:2と完全五度2:3のピタゴラス音階に長三度4:5を取り入れ簡単な整数比同士は響きの相性が良いが、
転調に弱いといわれている。
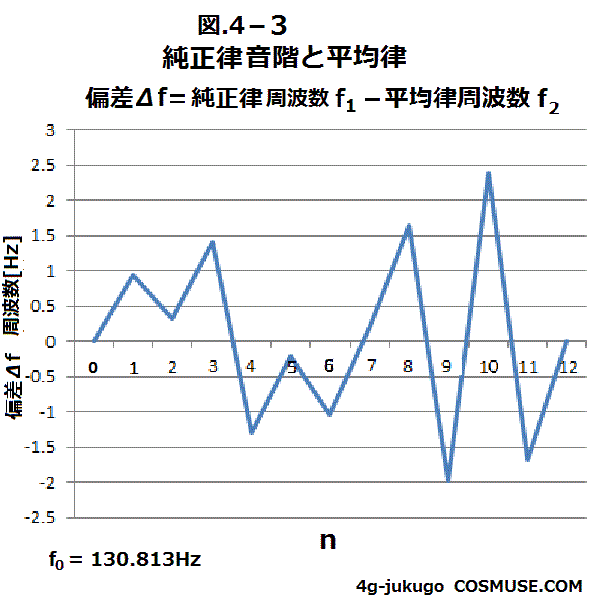
| イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | い |
| a | a# | b | c | c# | d | d# | e | f | f# | g | g# | a’ |
| ラ | ラ# | シ | ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ら |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 45/32 | 3/2 | 8/5 | 5/3 | 9/5 | 15/8 | 2 |
| 440.000 | 469.333 | 495.000 | 528.000 | 550.000 | 586.666 | 618.750 | 660.000 | 704.000 | 733.333 | 792.000 | 825.000 | 880.000Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4-3-2.C(ド)からはじまる純正律
鍵盤楽器は、c(ド)を中心にすることが多い。| ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ | は |
| c | c# | d | d# | e | f | f# | g | g# | a | a# | b | c’ |
| ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | ド |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 45/32 | 3/2 | 8/5 | 5/3 | 9/5 | 15/8 | 2 |
| 261.626 | 279.067 | 294.329 | 313.951 | 327.032 | 348.834 | 367.911 | 392.439 | 418.601 | 436.043 | 470.926 | 490.548 | 523.252Hz |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4-3-3. E(ミ)からはじまる純正律
ギターは、EADGBEにチューニングすることが多い。弦の長さcm| ホ | ヘ |
嬰へ 変ト | ト |
嬰ト 変イ | イ |
嬰イ 変ロ | ロ | ハ |
嬰ハ 変ニ | ニ |
嬰二 変ホ | ほ |
| e | f | f# | g | g# | a | a# | b | c | c# | d | d# | e’ |
| ミ | ファ | ファ# | ソ | ソ# | ラ | ラ# | シ | ド | ド# | レ | レ# | ミ |
| 1 | 16/15 | 9/8 | 6/5 | 5/4 | 4/3 | 45/32 | 3/2 | 8/5 | 5/3 | 9/5 | 15/8 | 2 |
| 329.628 | 351.603 | 370.831 | 395.553 | 412.035 | 439.504 | 463.539 | 494.442 | 527.404 | 549.380 | 593.330 | 618.052 | 659.256Hz |
| 630.000 | 590.625 | 560.000 | 525.000 | 504.000 | 472.500 | 448.000 | 420.000 | 393.750 | 378.000 | 350.000 | 336.000 | 315.000cm |
| 半音0 | 半音1 | 半音2 | 半音3 | 半音4 | 半音5 | 半音6 | 半音7 | 半音8 | 半音9 | 半音10 | 半音11 | 半音12 |
| 完全一度 | 短二度 | 長二度 | 短三度 | 長三度 | 完全四度 | 増四度/減五度 | 完全五度 | 短六度 | 長六度 | 短七度 | 長七度 | 八度 |
4−4.素数音階
素数音階を考えてみる。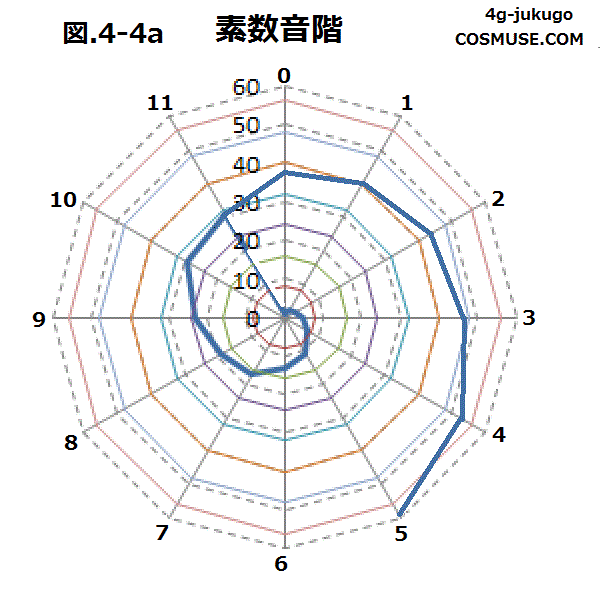
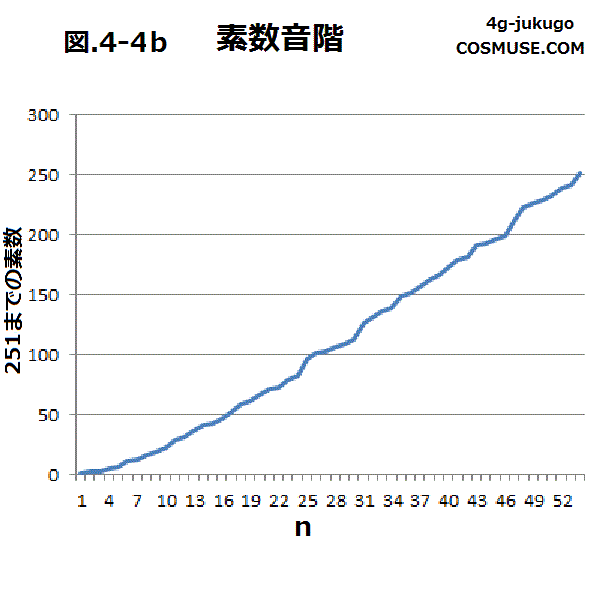
| 素数 | 1 | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 |
| 周波数 | 130.813 | 261.626 | 392.439 | 654.065 | 915.691 | 1438.943 | 1700.569 | 2223.821 | 2485.447 | 3008.699 | 3793.577 | 4055.203Hz |
| 1/oct | 1 | 1 | 1/2 | 1/4 | 1/4 | 1/8 | 1/8 | 1/16 | 1/16 | 1/16 | 1/16 | 1/16 |
| 周波数 | 130.813 | 261.626 | 196.219 | 163.516 | 228.922 | 179.867 | 212.571 | 138.988 | 155.340 | 188.043 | 237.098 | 253.4501875Hz |
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 周波数 | 130.813 | 138.988 | 151.252 | 155.340 | 163.516 | 179.867 | 188.043 | 196.219 | 212.571 | 228.922 | 237.098 | 253.450 | 261.626Hz |
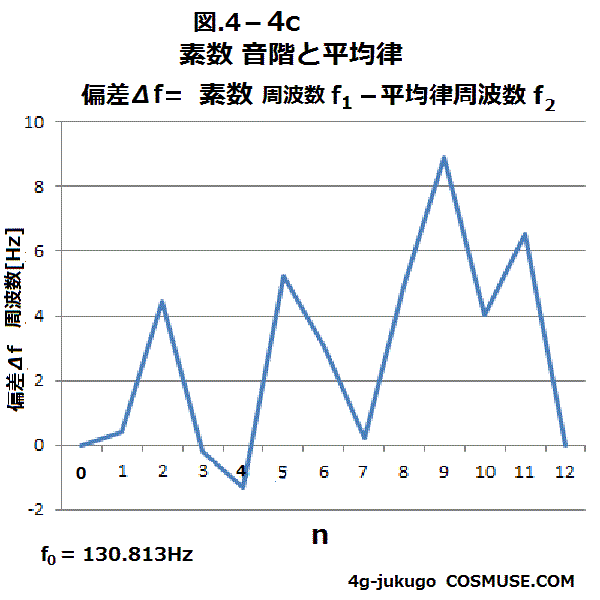
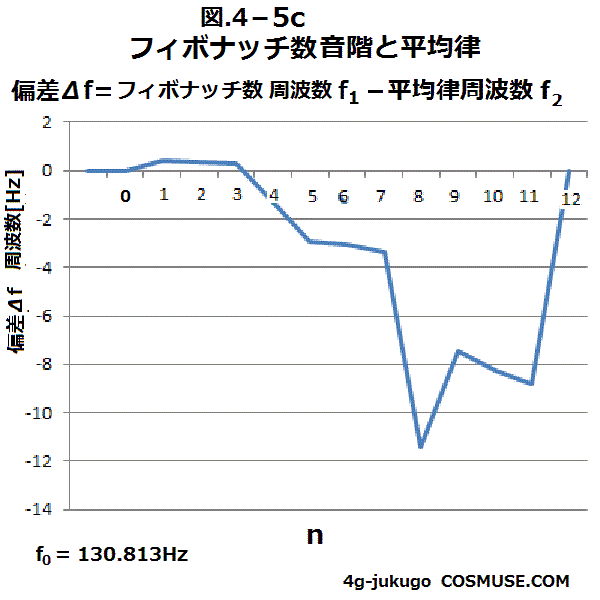
4−5.フィボナッチ音階
フィボナッチ音階を考えてみる。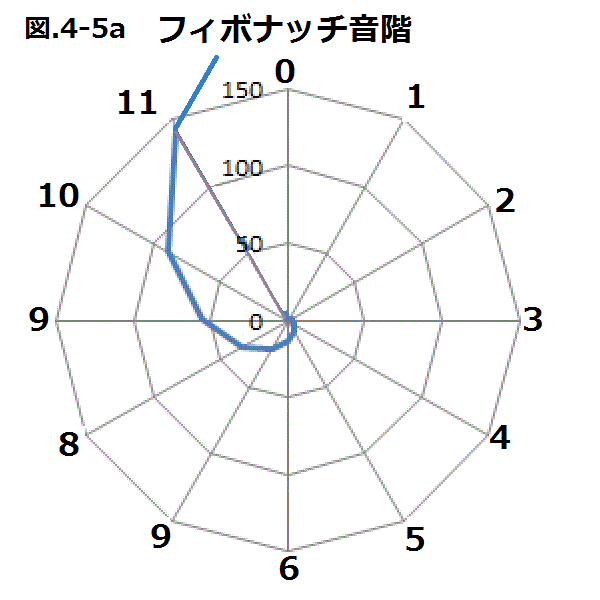
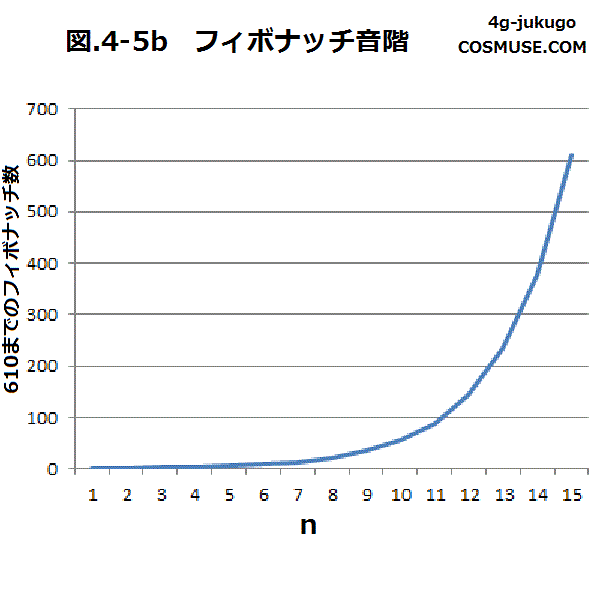
| FB数 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
| 周波数 | 130.813 | 130.813 | 261.626 | 392.439 | 654.065 | 1046.504 | 1700.569 | 2747.073 | 4447.642 | 7194.715 | 11642.357 | 18837.072 | 30479.429 | 49316.501 | 79795.93Hz |
| 1/oct | 1 | 1 | 1 | 1/2 | 1/4 | 1/4 | 1/8 | 1/16 | 1/32 | 1/32 | 1/64 | 1/128 | 1/128 | 1/256 | 1/512 |
| 周波数 | 130.813 | 130.813 | 261.626 | 196.219 | 163.516 | 261.626 | 212.571 | 171.692 | 138.988 | 224.834 | 181.911 | 147.164 | 238.120 | 192.642 | 155.851Hz |
| n | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 周波数 | 130.813 | 130.813 | 138.988 | 147.164 | 155.851 | 163.516 | 171.692 | 181.911 | 192.642 | 196.216 | 212.571 | 224.834 | 238.12 | 261.626Hz |
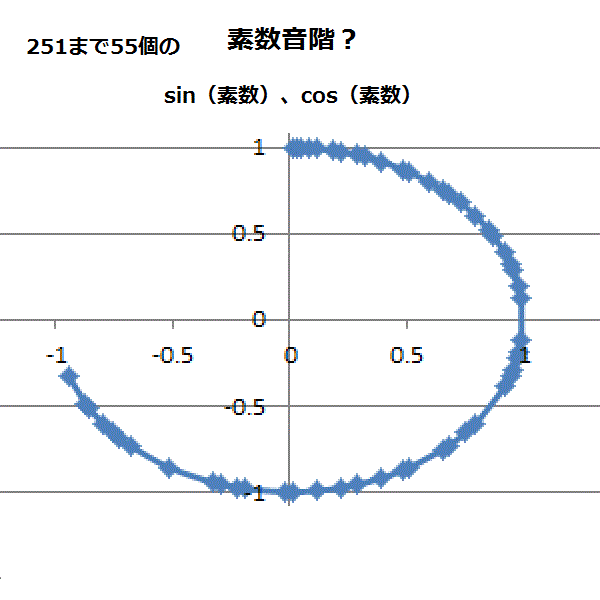
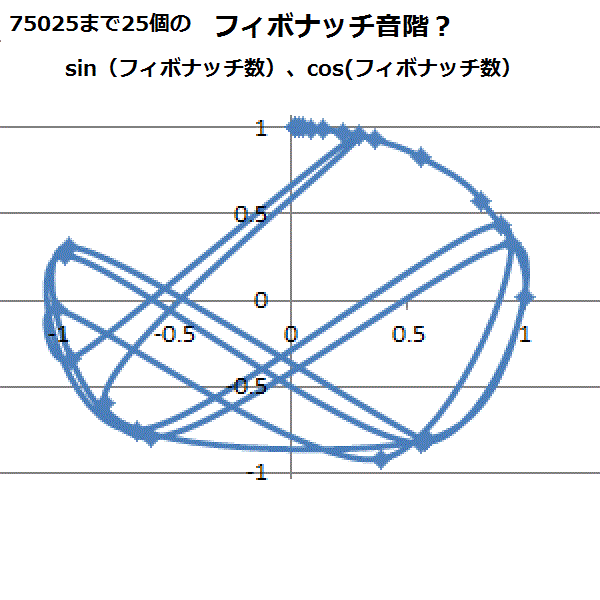
4−5.単位円の中へプロット
sin(素数)、cos(素数)の組み合わせと、sin(フィボナッチ数)、cos(フィボナッチ数)の組み合わせを単位円の図にしてみた。4-5-1.単位円内素数
4-5-2.単位円内フィボナッチ数
4−6.ギターフレット上の素数音階とフィボナッチ音階とそれぞれの植木算音階。
